DML GATE Example#

This notebook demonstrates how to estimate Group Average Treatment Effects (GATE) using Double Machine Learning. GATE allows us to understand treatment effect heterogeneity by estimating the average effect within specific groups defined by covariates.

Mathematical Formulation#

Let \(Y\) be the outcome, \(D\) the binary treatment, and \(X\) the covariates. We define the Conditional Average Treatment Effect (CATE) as:

\[ \tau(X) = \mathbb{E}[Y(1) - Y(0) \mid X] \]

For a set of groups \(G_1, \dots, G_K\) (where \(G_k(X)\) is an indicator that unit falls into group \(k\)), the GATE for group \(k\) is:

\[ \theta_k = \mathbb{E}[\tau(X) \mid G_k(X)=1] \]

We will:

  1. Generate synthetic data with heterogeneous treatment effects.

  2. Perform Exploratory Data Analysis (EDA).

  3. Estimate GATEs using gate_esimand with both automatic quantile groups and custom user-defined groups.

Generate data#

We generate observational data with a nonlinear outcome model, nonlinear treatment assignment, and a heterogeneous (nonlinear) treatment effect \(\tau(X)\).

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from causalis.data import CausalDatasetGenerator, CausalData

# Reproducibility
np.random.seed(42)

# 1) Confounders and their distributions
confounder_specs = [
    {"name": "tenure_months",     "dist": "normal",   "mu": 24, "sd": 12},
    {"name": "avg_sessions_week", "dist": "normal",   "mu": 5,  "sd": 2},
    {"name": "spend_last_month",  "dist": "uniform",  "a": 0,   "b": 200},
    {"name": "premium_user",      "dist": "bernoulli","p": 0.25},
    {"name": "urban_resident",    "dist": "bernoulli","p": 0.60},
]

# Indices
TENURE, SESS, SPEND, PREMIUM, URBAN = range(5)

# 2) Nonlinear baseline for outcome f_y(X) = X @ beta_y + g_y(X)
beta_y = np.array([0.03, 0.20, 0.01, 1.20, 0.60], dtype=float)

def g_y(X: np.ndarray) -> np.ndarray:
    tenure_years = X[:, TENURE] / 12.0
    sessions = X[:, SESS]
    spend = X[:, SPEND]
    premium = X[:, PREMIUM]
    urban = X[:, URBAN]
    return (
        1.2 * np.sin(2.0 * np.pi * tenure_years)
        + 0.02 * (sessions - 5.0) ** 2
        + 0.0015 * (spend - 100.0) * (sessions - 5.0)
        + 0.4 * premium * (sessions - 5.0)
        + 0.3 * urban * np.tanh((spend - 100.0) / 50.0)
    )

# 3) Nonlinear treatment score f_t(X) = X @ beta_t + g_t(X)
beta_d = np.array([0.010, 0.12, 0.001, 0.80, 0.25], dtype=float)

def g_d(X: np.ndarray) -> np.ndarray:
    tenure_years = X[:, TENURE] / 12.0
    sessions = X[:, SESS]
    spend = X[:, SPEND]
    premium = X[:, PREMIUM]
    urban = X[:, URBAN]
    soft_spend = 1.2 * np.tanh((spend - 80.0) / 40.0)
    return (
        0.6 * soft_spend
        + 0.15 * (sessions - 5.0) * (tenure_years - 2.0)
        + 0.25 * premium * (urban - 0.5)
    )

# 4) Heterogeneous, nonlinear treatment effect tau(X)
def tau_fn(X: np.ndarray) -> np.ndarray:
    tenure_years = X[:, TENURE] / 12.0
    sessions = X[:, SESS]
    spend = X[:, SPEND]
    premium = X[:, PREMIUM]
    urban = X[:, URBAN]
    tau = (
        1.0
        + 0.8 * (1.0 / (1.0 + np.exp(-(sessions - 5.0))))
        + 0.5 * premium
        - 0.6 * np.clip(tenure_years / 5.0, 0.0, 1.0)
        + 0.2 * urban * (spend - 100.0) / 100.0
    )
    return np.clip(tau, 0.2, 2.5)

# 5) Noise and prevalence
sigma_y = 3.5
target_d_rate = 0.35

# 6) Build generator
gen = CausalDatasetGenerator(
    outcome_type="continuous",
    sigma_y=sigma_y,
    target_d_rate=target_d_rate,
    seed=42,
    confounder_specs=confounder_specs,
    beta_y=beta_y,
    beta_d=beta_d,
    g_y=g_y,
    g_d=g_d,
    tau=tau_fn,
)

# 7) Generate data
n = 10000
generated_df = gen.generate(n)

# Ground-truth ATT
true_att = float(generated_df.loc[generated_df["d"] == 1, "cate"].mean())
print(f"Ground-truth ATT from the DGP: {true_att:.3f}")

# 8) Wrap as CausalData
causal_data = CausalData(
    df=generated_df,
    treatment="d",
    outcome="y",
    confounders=[
        "tenure_months",
        "avg_sessions_week",
        "spend_last_month",
        "premium_user",
        "urban_resident",
    ],
)

causal_data.df.head()

Ground-truth ATT from the DGP: 1.386
y d tenure_months avg_sessions_week spend_last_month premium_user urban_resident
0 2.237316 0.0 27.656605 5.352554 72.552568 1.0 0.0
1 5.771469 0.0 11.520191 6.798247 188.481287 1.0 0.0
2 6.374653 1.0 33.005414 2.055459 51.040440 0.0 1.0
3 2.364177 1.0 35.286777 4.429404 166.992239 0.0 1.0
4 8.378079 0.0 0.587578 6.658307 179.371126 0.0 0.0

EDA#

from causalis.eda import CausalEDA
eda = CausalEDA(causal_data)
eda.outcome_stats()
eda.outcome_hist()
eda.outcome_boxplot()
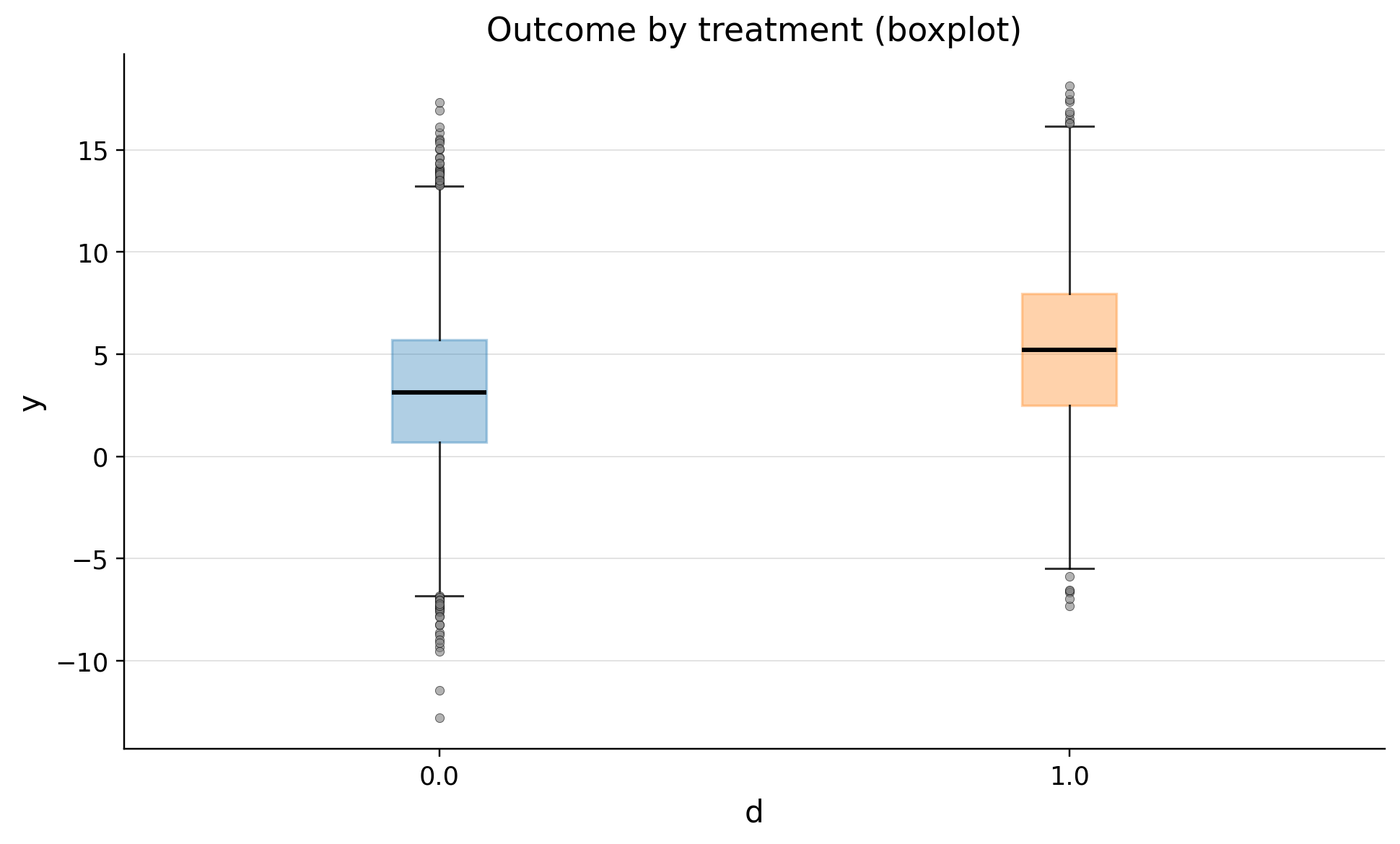
../_images/7605b9ef925a0f5b074c65f98fc1af0f8065237ff5a0be3b91674415fbb18135.png ../_images/7605b9ef925a0f5b074c65f98fc1af0f8065237ff5a0be3b91674415fbb18135.png

Inference: Estimating GATE#

We use gate_esimand to estimate Group Average Treatment Effects. This function works by leveraging the orthogonal signal from the DoubleML framework.

Methodology#

  1. Orthogonal Signal: We fit a DoubleML IRM model to obtain a score \(\psi(W;\hat{\eta})\) such that:

    \[ \mathbb{E}[\psi(W; \hat{\eta}) \mid X] \approx \tau(X) \]

    where \(W = (Y, D, X)\) and \(\hat{\eta}\) are the estimated nuisance parameters.

  2. Best Linear Predictor (BLP): We assume a linear model for the CATE using group indicators \(G(X)\):

    \[ \tau(X) \approx \sum_k \theta_k G_k(X) \]

    We estimate coefficients \(\theta\) by solving the BLP optimization:

    \[ \hat{\theta} = \arg\min_{\theta} \sum_{i=1}^N (\psi(W_i) - \theta^\top G(X_i))^2\]

When \(G(X)\) consists of mutually exclusive group indicators, \(\hat{\theta}_k\) corresponds to the average of the orthogonal signal within group \(k\), providing a consistent estimate of the GATE.

from causalis.inference.gate.gate_esimand import gate_esimand

1. GATE by CATE Quantiles#

If no groups are provided, gate_esimand automatically creates groups based on quantiles of the estimated CATE (Conditional Average Treatment Effect).

# Estimate GATE with 5 quantile groups
gate_quantiles = gate_esimand(causal_data, n_groups=5, confidence_level=0.95)

print("GATE Results (Quantiles):")
display(gate_quantiles)

GATE Results (Quantiles):
group n theta std_error p_value ci_lower ci_upper
0 Group_0 2000 1.376851 0.212620 9.441200e-11 0.960123 1.793579
1 Group_1 2000 0.899152 0.196052 4.512072e-06 0.514896 1.283408
2 Group_2 2000 1.114911 0.194088 9.226342e-09 0.734507 1.495316
3 Group_3 2000 1.190621 0.188706 2.801072e-10 0.820765 1.560478
4 Group_4 2000 1.332698 0.207103 1.235086e-10 0.926784 1.738612

2. GATE by User-Defined Groups#

We can also define custom groups based on covariates. For example, let’s group users by their tenure:

  • < 1 year

  • 1-3 years

  • > 3 years

# Define custom groups
tenure = causal_data.df['tenure_months']
groups = pd.cut(tenure, bins=[-np.inf, 12, 36, np.inf], labels=['<1y', '1-3y', '>3y'])

# Estimate GATE
gate_custom = gate_esimand(causal_data, groups=groups, confidence_level=0.95)

print("GATE Results (Tenure Groups):")
display(gate_custom)

GATE Results (Tenure Groups):
group n theta std_error p_value ci_lower ci_upper
0 tenure_months_1-3y 6785 1.187370 0.107453 2.189553e-28 0.976765 1.397974
1 tenure_months_<1y 1649 1.231591 0.221586 2.727795e-08 0.797290 1.665891
2 tenure_months_>3y 1566 1.104541 0.221472 6.123645e-07 0.670464 1.538617 
# Plot the results
plt.figure(figsize=(10, 6))

# Calculate error bars (distance from the mean)
yerr = [
    gate_custom['theta'] - gate_custom['ci_lower'],
    gate_custom['ci_upper'] - gate_custom['theta']
]

plt.errorbar(
    x=gate_custom['group'].astype(str),
    y=gate_custom['theta'],
    yerr=yerr,
    fmt='o',
    capsize=5,
    label='GATE Estimate'
)

plt.axhline(0, color='gray', linestyle='--', alpha=0.7)
plt.xlabel('Group')
plt.ylabel('GATE')
plt.title('Group Average Treatment Effects (Custom Groups)')
plt.legend()
plt.grid(axis='y', alpha=0.3)
plt.show()
On this page